2019-03-08

ディラック方程式を共変形式っぽい形に直す

ディラック方程式は、相対論的量子力学における方程式である。

つまり、相対論の観点からすると、ディラック方程式は、ローレンツ変換に対して形をかえない式として表すことができるはずである。

「ディラック方程式がローレンツ変換にたいして形を変えない（共変形式）」という要求に従って、二つの慣性系から見たスピノル同士の変換則が要求されることになる。

１．ディラック方程式を、共変形式っぽい形に直す

２．共変形式っぽい形が本当に共変形式であるようなスピノルの変換則がひとつだけ見つかる

の順番で、二つの慣性系からみたスピノル同士の変換則が導かれる。（そのスピノルの変換則は、四元ベクトルの変換則（座標同士のローレンツ変換と一緒）とは異なるということが計算で導かれる）

その過程において、今回は、「１．ディラック方程式を共変形式っぽい形に直す」ということに関して説明していきたいと思う。

ディラック方程式を共変形式っぽい形に直す

数式群（A）

$\begin{align} &\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &\alpha_{x, y, z}=\left( \begin{array}{cc}{0} & {\sigma_{x, y, z}} \\ {\sigma_{x, y, z}} & {0}\end{array}\right), \quad \beta=\left( \begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right),\beta^2=1\\ &\sigma_x=\left( \begin{array}{cc}{0} & {+1} \\ {+1} & {0}\end{array}\right), \quad \sigma_{y}=\left( \begin{array}{cc}{0} & {-i} \\ {+i} & {0}\end{array}\right) , \quad \sigma_{z}=\left( \begin{array}{cc}{+1} & {0} \\ {0} & {-1}\end{array}\right)\\ &\beta\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &\gamma^{0}=\beta, \quad \gamma^{1}=\beta \alpha_{x}, \quad \gamma^{2}=\beta \alpha_{y}, \quad \gamma^{3}=\beta \alpha_{z}\\ &\left(i \gamma^{\mu} \frac{\partial}{\partial x^{\mu}}-m\right) \psi(x)=0\\ &\beta\left(i \gamma^{\mu} \frac{\partial}{\partial x^{\mu}}-m\right) \psi(x)=\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &(1)\Leftrightarrow(6) \end{align}$

（１）はディラック方程式である。（ψはスピノル）

ここで、α、βなどは、（２）、（３）である。

（４）は（１）の両辺にβをかけたもの。

（４）において、（５）としてディラック表示でのガンマ行列とよばれるものを導入し、β＾２＝１を用いると、

（６）の式になる。(（１）から（６）の式が導かれる）

また、逆に、（６）の式にβをかけると、（７）になり、（１）の式が導かれる。

（（６）から（１）の式が導かれる）

つまり、（１）から（６）の式が導け、（６）から（１）の式が導けるという事は、（８）のように、（１）と（６）は同値であるということになる。

（８）は共変形式っぽい見た目をしている。

（８）が実際に共変形式であるためには、あるスピノルの変換則が要求されることになる。その計算は今回は触れないが、計算で導かれたスピノルの変換則は、四元ベクトルの変換則と異なるという結果になる。

ここで、ガンマ行列はローレンツ変換のもとで変わらない。特殊相対性理論における、「物理法則はローレンツ変換のもとで形を変えない方程式になる」という仮定は、「時間や空間、電場や磁場などの物理的な量がローレンツ変換のもとで形を変えても、物理法則の形が変わらないように式を書くことができる」ということである。変換されるのは、あくまで物理的な量である。物理的な状態である、ψなどがローレンツ変換のもとで変換されるのは分かるが、ローレンツ変換のもとで、（８）の方程式の係数であるガンマ行列が変わってしまうと、それは、方程式そのものの形が変わってしまった、ということになってしまう。

従って、ガンマ行列に関してはローレンツ変換のもとで形を変えないことが最初から要求される。

今回の記事はこれで終わりです。

過去の記事

feynmandiagram.hatenablog.com

2019-03-07

同次形の微分方程式の例題（xdx+ydy=mydx)

物理学

前回、こちらの記事で、同次形の微分方程式ならば変数分離することが出来て積分計算により微分方程式の解を求めることが出来るということについて触れました。

feynmandiagram.hatenablog.com

今回は同次形の微分方程式の例題について解いていきたいと思います。

今回解く同次形の微分方程式

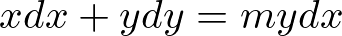
$\begin{align*} xdx+ydy&=mydx \end{align*}$

ｍは任意の実数です。

微分方程式を変数分離して解く

数式群（A）

$\begin{align} xdx+ydy&=mydx\\ y&=ux\\ dy&=udx+xdu\\ xdx+ux(udx+xdu)&=muxdx\\ x(1+u^2-mu)dx&=-ux^2du\\ \frac{d x}{x}&=\frac{u d u}{m u-1-u^{2}}\nonumber\\ &=\frac{-u d u}{1-m u+u^{2}}\nonumber\\ &=\frac{\left(-u+\frac{1}{2} m\right) d u}{1-m u+u^{2}}-\frac{\frac{1}{2} m d u}{1-m u+u^{2}}\\ \int \frac{d x}{x}&=\int \frac{-u+\frac{1}{2} m}{1-m u+u^{2}} d u-\int \frac{\frac{1}{2} m}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\\ \ln x&=-\frac{1}{2} \ln \left(u^{2}-m u+1\right)-\frac{m}{2} \int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\\ A &\equiv \int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u \end{align}$

（１）は今回解く微分方程式。

（２）は変数分離するためのuの導入。（前の記事で説明した）

（３）は（２）より導かれる関係式。

（４）は（２）、（３）を（１）に代入したもの。

（５）は（４）を整理したもの。

（６）は（４）を変数分離したもの。

（７）は（６）の両辺を積分したもの。

（８）は（７）の両辺を計算したもの。

（９）は（８）の右辺２項目に出てくる積分をAと定義した。

（９）のAさえ求まれば微分方程式の解が求まるのだが、

（９）のAは、４－ｍ＾２の符号によって、計算方法が変わってくる。

Aを４－ｍ＾２の符号によって場合分けしながら、計算していこう。

（i）4-m^2<０の時

数式群（B）

$\begin{align} A&=\int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\nonumber\\ &=\int \frac{1}{\left(u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}\right)\left(u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}\right)} d u\nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \int\left(\frac{1}{u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}}-\frac{1}{u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}}\right) d u\nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \ln \frac{u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}}{u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}}-\frac{2}{m}\ln c \nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \ln \frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}-\frac{2}{m}\ln c\\ \ln x &\sqrt{1-m u+u^{2}}+\frac{m}{2 \sqrt{m^{2}-4}} \ln \frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}=\ln c\\ &\left(\frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}\right)^{\frac{m}{2\sqrt{m^{2}-4}}} \sqrt{x^{2}-m x y+y^{2}}=c \end{align}$

（１）は（A-9）のAの計算。（-(2/m)lnc は積分定数）

（１）を（A-8）に代入して整理すると、（２）の式になる。

（２）にu=y/xを代入して左辺と右辺のｌｎの中身を比較することで、（３）の式を得る。

（３）が微分方程式の一般解である。（4-m^2<0の時）

（ii）4-m^2>0の時

数式群（C）

$\begin{align} \int \frac{d X}{X^{2}+A^{2}}&=\frac{1}{A} \arctan \frac{X}{A}\\ A&=\int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\nonumber\\ &=\frac{2}{\sqrt{4-m^{2}}} \arctan \frac{2 u-m}{\sqrt{4-m^{2}}}-\frac{2}{m} C\nonumber\\ &=\frac{2}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}}-\frac{2}{m} C\\ \log x \sqrt{1-m u+u^{2}}&=C-\frac{m}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}}\\ \log \sqrt{x^{2}-m x y+y^{2}}&=C-\frac{m}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}} \end{align}$

（１）は公式。

（２）は、（１）の公式をもとに、（A-9)のAを計算したもの。（最後の式でu=y/xを代入している）（-(2/m)Cは積分定数）

（３）は（２）を（A-8)に代入して整理したもの。

（４）は（３）においてu=y/xを代入したもの。

（４）が微分方程式の一般解である。（4-m^2>0の時）

(iii)4-m^2=0の時

数式群（D）

$\begin{align} \frac{d x}{x}&=\pm \frac{d u}{1\mp u}\mp \frac{d u}{(1\mp u)^{2}}\ \ (m=\pm2)\\ \log x&=C-\log (1\mp u)-\frac{1}{1\mp u}\\ \log x(1\mp u)&=C-\frac{1}{1\mp u}\\ \log (x\mp y)&=C-\frac{x}{x\mp y} \end{align}$

（１）は（A-6)をｍ＝±２の場合に計算したもの。

（２）は（１）の両辺を積分したもの。

（３）は（２）を整理したもの。

（４）は（３）にu=y/xを代入したもの。

（４）が微分方程式の一般解である。（4-m^2=0の時）

まとめ

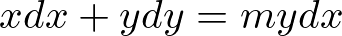
$\begin{align*} xdx+ydy&=mydx \end{align*}$

(mは任意の実数)

この微分方程式の一般解は、

4-m^2<0(m>2,m<-2）の時、(B-3)

4-m^2>0(-2<0>2）の時、（C-4)

4-m^2=0(m=±2)の時、（D-4）

である。

過去の記事

feynmandiagram.hatenablog.com

2019-03-06

ディラック方程式は負エネルギー解の問題を解決しない

物理学

クライン・ゴルドン方程式では、確率保存則の式が上手く作れないという問題と、負エネルギー解の問題がある。

以前の記事で書いたように、ディラックの方程式は、確率保存則の問題を解決する。

feynmandiagram.hatenablog.com

しかし、ディラックの方程式は負エネルギー解の問題を解決することが出来ない。

今回はそのことについて説明していきたいと思う。

ディラック方程式は負エネルギー解の問題を解決しない

ディラック方程式は負エネルギー解の問題を解決しない

数式群（A）

$\begin{align} &i \frac{\partial}{\partial t} \psi(x, t)=-i \bm{\alpha}\cdot \nabla \psi(x, t)+m \beta \psi(x, t)\\ &\psi(x)=w(p) e^{-i p x}\ \ \ (px\equiv Et-\bm{p}\cdot\bm{x})\\ &(E-\bm{\alpha}\cdot \bm{p}-m \beta) w(p)=0\\ &\omega(p)\neq0\to |E-\bm{\alpha}\cdot \bm{p}-m \beta|=\left| \begin{array}{cc}{E-m} & {-\bm{p}\cdot \bm{\sigma}} \\ {-\bm{p}\cdot \bm{\sigma}} & {E+m}\end{array}\right|=0\\ &p \equiv|\boldsymbol{p}|,\bm{p}=(0,0, p)\\ &\left| \begin{array}{cccc}{E-m} & {0} & {-p} & {0} \\ {0} & {E-m} & {0} & {p} \\ {-p} & {0} & {E+m} & {0} \\ {0} & {p} & {0} & {E+m}\end{array}\right|\nonumber\\ &=(E-m) \left| \begin{array}{ccc}{E-m} & {0} & {p} \\ {0} & {E+m} & {0} \\ {p} & {0} & {E+m}\end{array}\right|-p \left| \begin{array}{ccc}{0} & {-p} & {0} \\ {E-m} & {0} & {p} \\ {p} & {0} & {E+m}\end{array}\right|\nonumber\\ &=\left(E^{2}-p^{2}-m^{2}\right)^{2}\nonumber\\ &=\left(E^{2}-\bm{p}^{2}-m^{2}\right)^{2}=0\\ &E=\sqrt{\bm{p}^{2}+m^{2}}\ \ or\ \ E=-\sqrt{\bm{p}^{2}+m^{2}} \end{align}$

（１）はｎ＝２のディラック方程式。（スピン1/2のフェルミオンを記述する方程式）

（２）は確定した運動量に対する平面波（ω(p)はスピノル）

（２）を（１）に代入すると、（３）を得る。

（３）において、ω(p)≠０より、係数行列の行列式が０でなくてはならない（（４））

（５）では平面波の運動量ベクトルの向きにｚ軸をとり、ｐを新たに定義しなおした。（このｐは（２）で用いたｐとは異なる）。

（５）をもとに（４）を計算すると、（６）のようになる。

（６）より、（７）が導かれる。

（７）では、負エネルギー解が存在する。

この二つのエネルギーに対する解は独立であり、この二つの解の重ね合わせで一般解を表現することになるので、負エネルギー解は必要。

したがって、負エネルギー解の問題は解決されていない。

今回の記事はこれで終わりです。

過去の記事

feynmandiagram.hatenablog.com

2019-03-06

スピンが量子力学に出てくる理由

物理学

一般化された角運動量は、軌道角運動量と、スピンに分けられます。

一般化された角運動量の演算子とは、

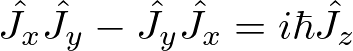
$\begin{align*} \hat{J_x}\hat{J_y}-\hat{J_y}\hat{J_x}=i\hbar\hat{J_z} \end{align*}$

を満たすような演算子Jのことを言います。

この交換関係を満たすような演算子Jの特徴は、波動関数に対し回転変換を施すことが出来るというものです。

また、この交換関係を満たすような演算子Jに対しては、方位量子数とよばれるものが整数または半整数になります。

ここで、軌道角運動量とスピンを分類する特徴をあげると、

軌道角運動量に対する固有関数が１価性をもつ（空間座標一つにつき一つの値をもつ）のにたいし、スピンに対しては１価性をもつような固有関数をつくることが出来ないという点にあります。

そういう観点から、軌道角運動量とスピンを分類すると、軌道角運動量は方位量子数が整数になり、スピンは方位量子数が半整数になります。

2019-03-05

ネットに価値を提供してもらってるようで提供しているのではないか。

意見

最近、思う事があります。

こういうブログとか、インターネットを使って、記事を書いて、それで広告で稼ぐなんていう人が多いですが、正直、ブログを書く労働に比べて、広告で２０万３０万稼ぐなんていうのはわりに合っていないと思います。

はてなブログとか、ワードプレスとか、Googleが開発したアプリとか、Twitterとか。

便利なものを使わせてもらっているようで、正直、使い手が運営側に提供する価値のほうが莫大なのではないのかと思います。

ブログ記事とか、書いてるけど、その価値って、Googleとかインターネット業者とかにほとんど吸い取られてると思います。

Twitterとかインスタグラムとかだって、みんなは儲けようと思ってやっているのではないのかもしれないけど、何かを書く、発信するという事は価値を生み出します。

それは自分にとっての価値にもなるけど、運営側がその価値をごっそりもっていっているような気がします。

だから、Googleの広告で稼げる！とか、アマゾンアソシエイトで儲けられる！とかいうのは一応あるけど、ブログ記事自体の価値ってのはそれで稼げる分より本来ははるかに高い可能性があると思います。

稼ぐなら、どこかから価値を横取りされないように稼いだほうがいいのかな。。。

2019-03-05

ディラック方程式が確率保存則の問題を解決する

物理学

今回は、ディラック方程式が、クライン・ゴルドン方程式での負の確率密度の問題を解決することについて説明します。

スピノル
ディラック方程式が確率保存則の問題を解決する

スピノル

数式群（A）

$\begin{align} i \frac{\partial}{\partial t} \psi(x, t)&=-i \boldsymbol{\alpha} \nabla \psi(x, t)+m \beta \psi(x, t)\ \ \ \ \ \left(\boldsymbol{\alpha}=\left(\alpha_{x}, \alpha_{y}, \alpha_{z}\right)\right)\\ \rho&=\psi^{*} \psi \rightarrow \psi^{\dagger} \psi\left(=\sum_{i=1}^{4} \psi_{i}^{*} \psi_{i} \geq 0\right)\\ \psi(\boldsymbol{x}, t)&=\left( \begin{array}{c}{\psi_{1}(\boldsymbol{x}, t)} \\ {\psi_{2}(\boldsymbol{x}, t)} \\ {\psi_{3}(\boldsymbol{x}, t)} \\ {\psi_{4}(\boldsymbol{x}, t)}\end{array}\right) \end{align}$

(1)はn=4のディラック方程式（スピン1/2のフェルミオンを記述するディラック方程式。）（αｘ、αｙ、αｚ、βは4行4列の行列）

（１）において、αｘ、αｙ、αｚ、βは4行４列の行列なので、ψは4行〇〇列にならなければならないが、確率密度を（２）のように拡張することを考えると、確率密度はスカラーにならなければいけないため、（３）のようにψは4行1列で表されることになる。

（３）をスピノルという。

ディラック方程式が確率保存則の問題を解決する

クライン・ゴルドン方程式では、確率保存則の式を作ろうとすると、確率密度が負の値もとりうることになってしまうという問題がある。

クライン・ゴルドン方程式の導出はこちら。

feynmandiagram.hatenablog.com

しかし、ディラック方程式はクライン・ゴルドン方程式の確率保存則の問題を解決する。

数式群（B）

$\begin{align} \frac{\partial}{\partial t} \psi(\boldsymbol{x}, t)&=-\boldsymbol{\alpha} \nabla \psi(\boldsymbol{x}, t)-i m \beta \psi(\boldsymbol{x}, t)\\ \frac{\partial}{\partial t} \psi^{\dagger}(\bm{x}, t)&=-\nabla \psi^{\dagger}(\bm{x}, t) \boldsymbol{\alpha}+i m \psi^{\dagger}(\bm{x}, t) \beta\\ \frac{\partial}{\partial t} \rho(\boldsymbol{x}, t)&=\left[\frac{\partial}{\partial t} \psi^{\dagger}(\boldsymbol{x}, t)\right] \psi(\boldsymbol{x}, t)+\psi^{\dagger}(\boldsymbol{x}, t)\left[\frac{\partial}{\partial t} \psi(\boldsymbol{x}, t)\right]\nonumber\\ &=-\left[\nabla \psi^{\dagger}(\boldsymbol{x}, t) \boldsymbol{\alpha}-i m \psi^{\dagger}(\boldsymbol{x}, t) \beta\right] \psi(\boldsymbol{x}, t)\nonumber\\ &\ \ \ \ \ \ -\psi^{\dagger}(\boldsymbol{x}, t)[\boldsymbol{\alpha} \nabla \psi(\boldsymbol{x}, t)+i m \beta \psi(\boldsymbol{x}, t)]\nonumber\\ &=-\left[\nabla \psi^{\dagger}(\boldsymbol{x}, t)\right] \boldsymbol{\alpha} \psi(\boldsymbol{x}, t)-\psi^{\dagger}(\boldsymbol{x}, t) \boldsymbol{\alpha}[\nabla \psi(\boldsymbol{x}, t)]\nonumber\\ &=-\operatorname{div}\left[\psi^{\dagger}(\boldsymbol{x}, t) \boldsymbol{\alpha} \psi(\boldsymbol{x}, t)\right]\\ j(\bm{x}, t)&=\psi^{\dagger}(\bm{x}, t) \boldsymbol{\alpha} \psi(\bm{x}, t)\\ \frac{\partial}{\partial t} \rho(\boldsymbol{x}, t)+\operatorname{div} j(\boldsymbol{x}, t)&=0 \end{align}$