2019-03-18

大学物理の内容を整理する

物理学

※偉そうな口調で書いていますが、自分の頭を整理するために書いているので、許してください。

力学

力学において重要なのは角運動量、慣性モーメント、連成調和振動子、微分方程式、など。

連成調和振動子では重心座標と相対座標に分けることで、連立微分方程式の対角化を行う事が出来る。

連立微分方程式を対角化を用いて解く、という手法を学んだりするため、線形代数との関連も深い。

他には、

空気抵抗とばねの力があるような系について、の減衰振動、臨界制動、過減衰

万有引力などの相互作用をする形について、換算質量を用いることで、問題を簡単に解く方法

運動量保存やエネルギー保存

微分方程式の解き方

などについて学ぶ。

微分方程式を解くというのが主要なテーマになるので、微分方程式の解き方だけでなく解き方の仕組みを抑えたり、線形代数を用いて連立微分方程式を解く手法を学んだり、（実対称行列は直交行列で対角化出来ることや、エルミート行列はユニタリー行列を用いて対角化出来ることも重要）積分計算をうまく出来るようにするべきである。（ヤコビアンがどのように導出されるかなど）

また、微分方程式を解くという観点でいえば、グリーン関数やフーリエ変換・ラプラス変換を用いた微分方程式の解き方を抑えておくべき。また、常微分方程式と偏微分方程式、線形微分方程式と非線形微分方程式など、きちんと分類分けをして、微分方程式の解き方を理解しているかも重要。

また、統計力学でも重要になるが、テイラー展開を用いた近似法についてもきちんと理解しておくべきである。（テイラー展開の導出は出来るかなど）

また、相対論的力学との違いについても、理解を深めておくべきだ。相対性理論は相対性理論、力学は力学だけで理解をするのではなく、なぜ力学だとこうで、相対論だとこうなるのかという点を理解しておくと、知識がごちゃごちゃにならない。慣性質量と重力質量の違いなども理解しておけば望ましい。

特に、調和振動子は、量子力学や統計力学、解析力学など、様々な分野との関連が深く、他の分野との対比の中で今後も理解していくべき事項。

電磁気学

電磁気学は、相対性理論や量子力学など、現代の物理学に深く関連している。

最も重要なのは、４つの方程式からなるマクスウェル方程式である。

それに加えてクーロンの法則と、重ね合わせの原理も、基本法則として重要である。

私の記憶ではクーロンの法則と、重ね合わせの原理、相対性理論を用いて、マクスウェル方程式を導くことができたと思う。（少し議論があいまいだったような気もしたが）

また、マクスウェルの方程式を導くうえで、ガウスの定理、ストークスの定理なども重要である。これらの定理の導出もできるようになっておくべき。また、ベクトル解析の公式に関しても、基本的な部分は抑えておくべきである。その際に注意すべき点は、ベクトルとナブラを同じようにベクトル解析の公式に当てはめると変な事になることがあるという事。ナブラはナブラで別のベクトル解析の公式があるので注意。

マクスウェルの方程式を用いて、電磁波の波動方程式を導く方法も出来るようになっておくべき。また、誘電体同士の境界面で電場、磁場などの接続条件がどうなるかを、マクスウェルの方程式を用いて考える方法もきちんと理解しておくべき。

電磁波については、TE波、TM波などの波について計算する方法や、境界面でどう屈折するかを表すスネルの法則や、反射の法則を導く方法についても理解しておくべき。電磁波は、振動と波動論との関連も深い。

（高校で雑に学んだ内容の伏線を回収していくことが大事）

また、ルジャンドル多項式や、球ベッセル関数は、量子力学などでも使うので、できれば理解しておくべき。

また、電位やベクトルポテンシャルを導入することで、電場や磁場を楽に計算することが出来ることがあることについても学んでおくべきである。ガウスの法則の微分形も問題を解くうえでは重要である。

他にも、電気双極子モーメントや磁気双極子モーメントの概念、磁気双極子モーメントがつくる磁束密度は微小電流ループがつくる磁束密度と同じであること、相対性理論によって電場から磁場が導かれること、相対論における電場と磁場の関係と、その関係がマクスウェル方程式を慣性系同士で不変にすること、を理解しておくべきである。

量子力学との関連でいえば、電磁気学で考えられる古典的な場の概念（電場とか磁場）をしっかりイメージでとらえておくと、場の量子論（そこでは場が量子化される）の勉強にもつながってくる。

また、電気回路でコンデンサー、コイルによって位相がどのように変化させられるのか、逆回路などの回路の組み方も理解しておくことが望ましい。

熱力学

熱力学では、微小量同士の関係を扱うという事が重要なテーマになる。

統計力学では、温度や、化学ポテンシャル、圧力などを、必要に応じてその物理的意味に合うように定義していき、量子力学との関連の中で、指数関数などを用いて様々な物理量（エネルギーなど）を数式として求めていく。

それに対し、熱力学では、基本的に、熱力学第一法則、第二法則をもとに、温度やエントロピー、体積、圧力などの微小量同士の関係を求めることが凄く重要（統計力学のように、値を数式で表すことも普通にあるが）。量子力学とあまり関連付けて学ばないため、対応できる状況の数は統計力学よりも少ないと思われる。また、エントロピーなども、物理的なイメージを伴わないまま、天下り的に定義し、それが状態量であるということを確認したうえで理論を進めていく。

具体的には、

ファンデル・ワールスの状態方程式

エントロピー増大則・不可逆変化・可逆変化

熱力学第０・第一・第二・第三法則

相転移

ヘルムホルツ・ギブスの自由エネルギー・エンタルピー・ルジャンドル変換・マクスウェルの関係式

示強変数・示量変数

ジュール・トムソン効果

色んな熱力学的関係式の導出

カルノーサイクルなどの熱機関

などについて学ぶ。

振動と波動

振動と波動という分野があるのは、振動、波動は、量子力学、場の量子論、解析力学、統計力学、力学、電磁気学、流体力学など、多岐にわたる分野で凄く重要になるからである。

振動と波動では、

連成調和振動子

基準振動

うなり

波動方程式（一次元、二次元、三次元）

フーリエ変換

群速度、位相速度

レンズでの回折（中学校で習った内容の複雑バージョン）

波の反射、透過

地震計やラジオ、テレビ電波などの原理

Q値

などについて学ぶ

波動方程式が最も重要で、その解の形がどのようになるかはきちんと押さえておくべき。また、群速度と位相速度がごっちゃにならないように気を付ける。

フーリエ変換は、他の分野でも凄く重要なので、振動と波動論を学ぶ機会に、導出まで完全に理解しておくべき。

また、連成調和振動子は、統計力学のアインシュタイン模型でも重要になってくるので、理解しておくべき

物理数学

物理数学で重要なのは、

線形代数

複素関数論（留数定理など）

フーリエ変換・ラプラス変換

微分方程式の解き方（グリーン関数など）

微分積分学

である。

これらは大学院入試の数学などで問われることも多いだろう。

これらの５つは、互いにつながっていて、

デルタ関数のフーリエ積分表示などには複素関数論が使われているし、線形代数でも複素数を用いた行列が扱われるし、微分方程式はフーリエ変換やラプラス変換を用いて解くといい時が良くあるし、微分積分学は微分方程式やフーリエ変換・ラプラス変換・複素関数論で重要だし。

それに加えてこれら５つのテーマは物理でめちゃくちゃ使われる。

線形代数と複素関数論はおもに量子力学で。

フーリエ変換・ラプラス変換はあらゆる分野で。（量子力学、振動と波動など）

微分方程式の解き方も、あらゆる分野で。

微分積分学も、あらゆる分野で（統計力学が一番使うと思う）

ただの数学と思って、全然勉強していないと、後々後悔すると思う。

解析力学

解析力学で最も重要なのは

オイラー・ラグランジュ方程式

ハミルトンの正準方程式（正準変換も重要）

の二つだと思う。オイラー・ラグランジュ方程式と、ハミルトンの正準方程式は等価だけど、どちらも重要。

束縛条件がある場合にどのようにして作用を定義するかや、対称性と保存則がどのように関連するか（ネーターの定理（場の量子論でも学ぶ））についても理解しておくべき。

なぜ解析力学では力学と等価であることをわざわざ色んな事して別の形で表そうとするのかというと、同じことでも色んな形で表すといろんな発想に繋がりやすいから。

現に、ポアソンの括弧式などはディラックの正準量子化などの考えにもつながってくる。

また、ニュートンの運動方程式で考えるよりも、オイラー・ラグランジュ方程式や、ハミルトンの正準方程式で問題を解いたほうが簡単に解けることも多い。

作用やハミルトニアン、ラグランジアンは、場の量子論でも同じように学ぶことになる。

統計力学

統計力学で最も重要なのは分配関数を使った、ミクロカノニカル分布、カノニカル分布、グランドカノニカル分布の理解である。

この方法そのものについて、きちんと理解しておけば、色んな状況に対応できる。

それに加えて、温度、圧力がどう定義されるか、や、アインシュタイン模型、デバイ模型、イジング模型、ボース・アインシュタイン凝縮、高温、低温極限で比熱などがどうふるまうか、バンド、古典統計力学近似と量子統計力学の手法の違いについても理解しておけば望ましい。

ラグランジュの未定係数法は解析力学でも学ぶが、統計力学でも重要である。

そのほかにも、エネルギー等分配則や、定性的な理解をすることが出来るか、フェルミ分布、ボース分布なども重要である。

量子力学との関連でいえば、境界条件によって運動量が量子化されることについても知っておくべき。

また、近似が統計力学においてはものすごく重要なので、どのような考え方で近似をしていくかについても学んでおくべき。

相対性理論

相対性理論で重要なのは、力学との違いを認識しながら学んでいくこと。

また、３次元で不変なものとしてベクトルがあったのに対し、相対性理論では時間と空間を同時に扱うために、４成分のテンソルが使われることが重要である。

相対性理論における式は全てテンソルで書かれ、慣性系同士のローレンツ変換に応じて式の形が変わらないようにテンソルが変換されることになる。

よく問題などで出されそうなのは、簡単なコンプトン散乱で運動量保存則、エネルギー保存則をどのように使うかなど。

また、テンソルの添え字の縮約や、反変ベクトル、共変ベクトルも重要である。

テンソルに関しては、相対論的量子力学や、連続体力学などでも使われることになるので、苦手意識を持たないように練習しておくべき。

４元速度や、４元加速度の物理的意味や、エネルギー・運動量テンソルや４元運動量に関する保存則についても理解しておくべきである。

一般相対性理論は、多様体でどのように平坦が定義されるか、や、どのような洞察に基づいてアインシュタイン方程式がみちびかれるか、を理解しているか、また、どこに仮定があるのかを理解していることが重要。

量子力学

量子力学で重要なのは

解析力学、統計力学（古典物理学）との関連性

演算子の行列表示

シュレディンガー方程式

交換関係と同時固有状態を作れるかどうかの関係

スピンや軌道角運動量（回転変換、並進変換についても）

位置表示と運動量表示での固有関数や位置演算子と運動量演算子

ハイゼンベルクの不確定性関係

統計力学の連成調和振動子を量子力学で表すとどうなるか

線形代数を用いた解法（対角化を用いて固有値、固有状態を求める、など）

交換関係の計算

コヒーレント状態

調和振動子

ブラ・ケット記法

相対論的量子力学の構成

完全系

物理量の期待値計算

近似法（摂動論など）

運動量、位置の固有関数

接続条件やパリティ、振動定理

シュレディンガー描像、ハイゼンベルク描像、朝永・ディラック描像でどのように状態、演算子が変化していくのか（行列、演算子が指数関数の肩についている場合にも慣れておくべき）

水素原子のクーロンポテンシャルやデルタ関数型ポテンシャル、調和振動子のポテンシャル、トンネル効果でのポテンシャル、箱型ポテンシャル、

など、代表的なポテンシャルに対し、定常状態でのハミルトニアンに対するエネルギー固有値、固有関数の求め方は、理解しておくべきである。

（調和振動子の基底状態の求め方は覚えておこう）また、調和振動子については、生成消滅演算子を用いたブラケット記法での考え方も理解しておくべき（場の量子論との関連も深い）

大学院入試の内容を自分で整理するために、大学院入試で出るような、習った内容についてまとめました。

基本的には自分のために書きましたが、誰かの役に立ったり、物理ってこんなことやるんやとしってもらえたりしたらうれしいです。

過去の記事。

feynmandiagram.hatenablog.com

2019-03-14

Windowsの機能、使いこなせてますか？

知っておくと役に立つこと

最近、Windowsに色んな機能があることをしって、結構便利だと思ったので、共有したいと思います。

Snipping tool

これ、ブロガーの人にとっては結構便利だと思います。

ブログにスクリーンショットの一部だけを載せたいことって多々あると思いますが、

それをこのSnipping toolを使って簡単にすることが出来ます。

Windows Vista/7/8/8.1/10に標準で搭載されています。

こんな感じでブログなどに載せたいところを切り取れば...

f:id:feynmandiagram:20190314080111p:plain

こういう感じですぐに画像が出来上がります。

f:id:feynmandiagram:20190314080252p:plain

出来上がった画像をコピペすれば

f:id:feynmandiagram:20190314080352p:plain

こうやって簡単に貼り付けられます。

ちょっと便利じゃない？

ペイント３D

ペイント３DはWindows10に標準で搭載されているソフトです。

www.microsoft.com

ペイント３Dの特徴は、３Dに絵を描くことが出来る！というもの。

でも、私は３D機能を使ったことないので、私のペイント３Dの使い方を紹介します（笑）。

ちょこっとお絵かきをしてブログに載せたいと思ったら、

お絵かきをした後、左上にある「選択」をクリックし、ブログに載せたいところを切り取ります。

f:id:feynmandiagram:20190314081512p:plain

切り取ったところをコピペすれば

f:id:feynmandiagram:20190314081432p:plain

こんな感じでお絵かきしたものを貼り付けられます。

パソコンだと使い方がよくわからない機能でも、ペイント３Dで手書きで書けば自由度が凄く増します。グラフとか、図とか、困ったら、ペイント３Dで書くのもありです。

後、手書きのほうが、親近感が増すかもしれません。こっちとしてはそんなに堅い気持ちで書いていない内容でも、パソコンで書いたものはお堅く見えやすいのではないかと思います。ニュアンスとかを正確に伝えるためにも、手書きって便利ですね！！

f:id:feynmandiagram:20190314082700p:plain

2019-03-13

検索流入の割合が３０%を超えました！【ブログ歴約３か月】

ブログ運営

f:id:feynmandiagram:20190313222720p:plain

わーいわーい。

検索流入がずっとほしかったのですが、徐々に検索流入が増えてきて、なんと検索流入が３０パーセントに到達しました。

たいしたことないかもしれませんが私にとっては凄くうれしいです。

f:id:feynmandiagram:20190313223135p:plain

どーん。

以前この記事で紹介したときは、

feynmandiagram.hatenablog.com

f:id:feynmandiagram:20190205083618p:plain

こんな感じで、検索流入はたったの４%でした。

ずっとその時から検索流入が欲しいといっていたので、検索流入が増えたのは素直にうれしいです。

しかし！！アクセス数自体は一向に伸びません！！

f:id:feynmandiagram:20190313223713p:plain

それもそのはずです。

スピノルの慣性系同士の変換

物理学

以前書いた記事

で、ディラック方程式を共変形式っぽい形に直す方法について説明した。

その共変形式っぽい形が実際に共変形式になるためには、ある、二つの慣性系から見たスピノルの変換則が要求されることについても話した。

今回は、その変換則を導く方法について説明したいと思う。

スピノルの変換が満たす条件を求める

数式群（A）

$\begin{align} &\psi^{\prime}\left(x^{\prime}\right)=S(\Lambda) \psi(x)\\ &\left(i \gamma^{\mu} \partial_{\mu}^{\prime}-m\right) \psi^{\prime}\left(x^{\prime}\right)=0, \quad\left(i \gamma^{\mu} \partial_{\mu}-m\right) \psi(x)=0\\ &\partial_{\mu}^{\prime}=\overline{\Lambda}_{\mu}^{\ \nu} \partial_{\nu}\\ &\left(i\overline{\Lambda}_{\mu}^{\ \nu} S^{-1}\gamma^{\mu}S\partial_{\nu} -m\right) \psi\left(x\right)=0\\ &\gamma^{\nu}=\overline{A}_{\mu}^{\ \nu} S^{-1} \gamma^{\mu} S\\ &\overline{\Lambda}_{\mu}^{\ \nu}=\left(\Lambda^{-1}\right)_{\ \mu}^{\nu}\\ &\gamma^{\mu}=\Lambda_{\ \nu}^{\mu} S(\Lambda) \gamma^{\nu} S^{-1}(\Lambda)\\ &\gamma^{\mu} \partial_{\mu}^{\prime} \psi^{\prime}\left(x^{\prime}\right)=S(\Lambda) \gamma^{\mu} \partial_{\mu} \psi(x) \end{align}$

スピノル同士の変換の形を（１）のようにおく。

（２）の二つの式が同時に成立するような（１）のSを見つけることが今回の目的。

（３）は偏微分のローレンツ変換。

（２）の左の式にS＾（－１）をかけ、（１）と（３）を代入すると、

（４）の式になる。

（４）と（２）の右の式を比較すると、（５）が分かる。（６）の関係を利用することで、（５）から（７）を得る。

（１）と（３）と（７）より、（８）の関係を得る。

（５）とか、（７）とか（８）が、スピノルの変換を引き起こす行列Sの条件である。（５）と（７）と（８）の条件はどれも同じなので、どの条件を用いてもよい。今後は（７）の条件を用いる。

Sが満たすべき条件から、Sを求める

微小ローレンツ変換を表すようなSに対して、（７）の条件を満たすようなSを見つけたら、それが求めるべきSである。

一般の変換は微小変換の積み重ねで得られるから、そのような条件を満たすならば任意の変換に対して（７）が満たされることが分かるのである。

数式群（B）

$\begin{align} &\Lambda_{\ \nu}^{\mu}=g_{\ \nu}^{\mu}(=\delta_{\nu}^{\mu})+\delta \omega_{\ \nu}^{\mu}\\ &x^{\prime \mu}=x^{\mu}+\delta \omega_{\ \nu}^{\mu} x^{\nu}\\ &g_{\mu \nu} x^{\prime \mu} x^{\prime \nu}=g_{\mu \nu} x^{\mu} x^{\nu}+\left(\delta \omega_{\mu \nu}+\delta \omega_{\nu \mu}\right) x^{\mu} x^{\nu}\\ &g_{\mu \nu} x^{\prime \mu} x^{\prime \nu}=g_{\mu \nu} x^{\mu} x^{\nu}\\ &\delta \omega_{\mu \nu}=-\delta \omega_{\nu \mu}\\ &\psi^{\prime}\left(x^{\prime}\right)=S(\Lambda) \psi(x)=\left(1+S^{\mu \nu} \delta \omega_{\mu \nu}\right) \psi(x)\\ &\left(\left[S^{\mu \nu}, \gamma^{\alpha}\right]+g^{\alpha \mu} \gamma^{\nu}\right) \delta \omega_{\mu \nu}=0\\ &\left[S^{\mu \nu}, \gamma^{\alpha}\right]+g^{\alpha \mu} \gamma^{\nu}=0\\ &2\left[S^{\mu \nu}, \gamma^{\alpha}\right]+g^{\alpha \mu} \gamma^{\nu}-g^{\alpha \nu} \gamma^{\mu}=0\\ &\sigma^{\mu \nu} \equiv \frac{1}{2} i\left[\gamma^{\mu}, \gamma^{\nu}\right]\\ &S^{\mu \nu}=-\frac{1}{4} i \sigma^{\mu \nu}\\ &S(\Lambda)=1-\frac{1}{4} i \sigma^{\mu \nu} \delta \omega_{\mu \nu} \end{align}$

（１）のように、微小なローレンツ変換の行列を考えると、

（２）のような座標変換が起きる。

ここで、（３）は（２）を利用して導いた関係であるが、ローレンツ変換のもとでの内積の不変性（４）より、（５）の反対称性が導かれる。

ここで、微小変換を引き起こす行列S＾（μν）を考え、（６）の関係式をつくる。ここで、δωが反対称という事から、S＾（μν）も反対称という事が分かる。

（６）を（A-7)に代入することで、（７）の関係式を得る。

（７）において、δωは任意の微小変換パラメータだから、（８）の関係式が導かれる。

（８）の関係式から、S＾（μν）が反対称であることを利用すると、（９）の式が得られる。

ここで、S＾（μν）が反対称であることから、Sの範囲に強い制限が加えられ、（１０）のようにおいたとき、（９）を満たすS^（μν）が（１１）ただ一つの形に限られることが計算によって導かれる。（ここの議論は自分では考えられないと思うけど、ここではしない。）

従って、ディラック方程式の形を微小ローレンツ変換によって変化させないために必要なスピノルの変換則を引き起こすSは、（１２）のみであることが分かる。

過去の記事

feynmandiagram.hatenablog.com

2019-03-08

ディラック方程式を共変形式っぽい形に直す

ディラック方程式は、相対論的量子力学における方程式である。

つまり、相対論の観点からすると、ディラック方程式は、ローレンツ変換に対して形をかえない式として表すことができるはずである。

「ディラック方程式がローレンツ変換にたいして形を変えない（共変形式）」という要求に従って、二つの慣性系から見たスピノル同士の変換則が要求されることになる。

１．ディラック方程式を、共変形式っぽい形に直す

２．共変形式っぽい形が本当に共変形式であるようなスピノルの変換則がひとつだけ見つかる

の順番で、二つの慣性系からみたスピノル同士の変換則が導かれる。（そのスピノルの変換則は、四元ベクトルの変換則（座標同士のローレンツ変換と一緒）とは異なるということが計算で導かれる）

その過程において、今回は、「１．ディラック方程式を共変形式っぽい形に直す」ということに関して説明していきたいと思う。

ディラック方程式を共変形式っぽい形に直す

数式群（A）

$\begin{align} &\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &\alpha_{x, y, z}=\left( \begin{array}{cc}{0} & {\sigma_{x, y, z}} \\ {\sigma_{x, y, z}} & {0}\end{array}\right), \quad \beta=\left( \begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right),\beta^2=1\\ &\sigma_x=\left( \begin{array}{cc}{0} & {+1} \\ {+1} & {0}\end{array}\right), \quad \sigma_{y}=\left( \begin{array}{cc}{0} & {-i} \\ {+i} & {0}\end{array}\right) , \quad \sigma_{z}=\left( \begin{array}{cc}{+1} & {0} \\ {0} & {-1}\end{array}\right)\\ &\beta\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &\gamma^{0}=\beta, \quad \gamma^{1}=\beta \alpha_{x}, \quad \gamma^{2}=\beta \alpha_{y}, \quad \gamma^{3}=\beta \alpha_{z}\\ &\left(i \gamma^{\mu} \frac{\partial}{\partial x^{\mu}}-m\right) \psi(x)=0\\ &\beta\left(i \gamma^{\mu} \frac{\partial}{\partial x^{\mu}}-m\right) \psi(x)=\left(i \frac{\partial}{\partial t}-\alpha_xp_{x}-\alpha_y p_{y}-\alpha_{z} p_{z}-\beta m\right)\psi=0\\ &(1)\Leftrightarrow(6) \end{align}$

（１）はディラック方程式である。（ψはスピノル）

ここで、α、βなどは、（２）、（３）である。

（４）は（１）の両辺にβをかけたもの。

（４）において、（５）としてディラック表示でのガンマ行列とよばれるものを導入し、β＾２＝１を用いると、

（６）の式になる。(（１）から（６）の式が導かれる）

また、逆に、（６）の式にβをかけると、（７）になり、（１）の式が導かれる。

（（６）から（１）の式が導かれる）

つまり、（１）から（６）の式が導け、（６）から（１）の式が導けるという事は、（８）のように、（１）と（６）は同値であるということになる。

（８）は共変形式っぽい見た目をしている。

（８）が実際に共変形式であるためには、あるスピノルの変換則が要求されることになる。その計算は今回は触れないが、計算で導かれたスピノルの変換則は、四元ベクトルの変換則と異なるという結果になる。

ここで、ガンマ行列はローレンツ変換のもとで変わらない。特殊相対性理論における、「物理法則はローレンツ変換のもとで形を変えない方程式になる」という仮定は、「時間や空間、電場や磁場などの物理的な量がローレンツ変換のもとで形を変えても、物理法則の形が変わらないように式を書くことができる」ということである。変換されるのは、あくまで物理的な量である。物理的な状態である、ψなどがローレンツ変換のもとで変換されるのは分かるが、ローレンツ変換のもとで、（８）の方程式の係数であるガンマ行列が変わってしまうと、それは、方程式そのものの形が変わってしまった、ということになってしまう。

従って、ガンマ行列に関してはローレンツ変換のもとで形を変えないことが最初から要求される。

今回の記事はこれで終わりです。

過去の記事

feynmandiagram.hatenablog.com

2019-03-07

同次形の微分方程式の例題（xdx+ydy=mydx)

物理学

前回、こちらの記事で、同次形の微分方程式ならば変数分離することが出来て積分計算により微分方程式の解を求めることが出来るということについて触れました。

feynmandiagram.hatenablog.com

今回は同次形の微分方程式の例題について解いていきたいと思います。

今回解く同次形の微分方程式

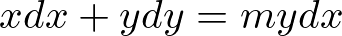
$\begin{align*} xdx+ydy&=mydx \end{align*}$

ｍは任意の実数です。

微分方程式を変数分離して解く

数式群（A）

$\begin{align} xdx+ydy&=mydx\\ y&=ux\\ dy&=udx+xdu\\ xdx+ux(udx+xdu)&=muxdx\\ x(1+u^2-mu)dx&=-ux^2du\\ \frac{d x}{x}&=\frac{u d u}{m u-1-u^{2}}\nonumber\\ &=\frac{-u d u}{1-m u+u^{2}}\nonumber\\ &=\frac{\left(-u+\frac{1}{2} m\right) d u}{1-m u+u^{2}}-\frac{\frac{1}{2} m d u}{1-m u+u^{2}}\\ \int \frac{d x}{x}&=\int \frac{-u+\frac{1}{2} m}{1-m u+u^{2}} d u-\int \frac{\frac{1}{2} m}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\\ \ln x&=-\frac{1}{2} \ln \left(u^{2}-m u+1\right)-\frac{m}{2} \int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\\ A &\equiv \int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u \end{align}$

（１）は今回解く微分方程式。

（２）は変数分離するためのuの導入。（前の記事で説明した）

（３）は（２）より導かれる関係式。

（４）は（２）、（３）を（１）に代入したもの。

（５）は（４）を整理したもの。

（６）は（４）を変数分離したもの。

（７）は（６）の両辺を積分したもの。

（８）は（７）の両辺を計算したもの。

（９）は（８）の右辺２項目に出てくる積分をAと定義した。

（９）のAさえ求まれば微分方程式の解が求まるのだが、

（９）のAは、４－ｍ＾２の符号によって、計算方法が変わってくる。

Aを４－ｍ＾２の符号によって場合分けしながら、計算していこう。

（i）4-m^2<０の時

数式群（B）

$\begin{align} A&=\int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\nonumber\\ &=\int \frac{1}{\left(u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}\right)\left(u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}\right)} d u\nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \int\left(\frac{1}{u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}}-\frac{1}{u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}}\right) d u\nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \ln \frac{u-\frac{m}{2}-\frac{\sqrt{m^{2}-4}}{2}}{u-\frac{m}{2}+\frac{\sqrt{m^{2}-4}}{2}}-\frac{2}{m}\ln c \nonumber\\ &=\frac{1}{\sqrt{m^{2}-4}} \ln \frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}-\frac{2}{m}\ln c\\ \ln x &\sqrt{1-m u+u^{2}}+\frac{m}{2 \sqrt{m^{2}-4}} \ln \frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}=\ln c\\ &\left(\frac{2 y-\left(m+\sqrt{m^{2}-4}\right) x}{2 y-\left(m-\sqrt{m^{2}-4}\right) x}\right)^{\frac{m}{2\sqrt{m^{2}-4}}} \sqrt{x^{2}-m x y+y^{2}}=c \end{align}$

（１）は（A-9）のAの計算。（-(2/m)lnc は積分定数）

（１）を（A-8）に代入して整理すると、（２）の式になる。

（２）にu=y/xを代入して左辺と右辺のｌｎの中身を比較することで、（３）の式を得る。

（３）が微分方程式の一般解である。（4-m^2<0の時）

（ii）4-m^2>0の時

数式群（C）

$\begin{align} \int \frac{d X}{X^{2}+A^{2}}&=\frac{1}{A} \arctan \frac{X}{A}\\ A&=\int \frac{1}{\left(u-\frac{m}{2}\right)^{2}+\frac{4-m^{2}}{4}} d u\nonumber\\ &=\frac{2}{\sqrt{4-m^{2}}} \arctan \frac{2 u-m}{\sqrt{4-m^{2}}}-\frac{2}{m} C\nonumber\\ &=\frac{2}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}}-\frac{2}{m} C\\ \log x \sqrt{1-m u+u^{2}}&=C-\frac{m}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}}\\ \log \sqrt{x^{2}-m x y+y^{2}}&=C-\frac{m}{\sqrt{4-m^{2}}} \arctan \frac{2 y-m x}{x \sqrt{4-m^{2}}} \end{align}$

（１）は公式。

（２）は、（１）の公式をもとに、（A-9)のAを計算したもの。（最後の式でu=y/xを代入している）（-(2/m)Cは積分定数）

（３）は（２）を（A-8)に代入して整理したもの。

（４）は（３）においてu=y/xを代入したもの。

（４）が微分方程式の一般解である。（4-m^2>0の時）

(iii)4-m^2=0の時

数式群（D）

$\begin{align} \frac{d x}{x}&=\pm \frac{d u}{1\mp u}\mp \frac{d u}{(1\mp u)^{2}}\ \ (m=\pm2)\\ \log x&=C-\log (1\mp u)-\frac{1}{1\mp u}\\ \log x(1\mp u)&=C-\frac{1}{1\mp u}\\ \log (x\mp y)&=C-\frac{x}{x\mp y} \end{align}$

（１）は（A-6)をｍ＝±２の場合に計算したもの。

（２）は（１）の両辺を積分したもの。

（３）は（２）を整理したもの。

（４）は（３）にu=y/xを代入したもの。

（４）が微分方程式の一般解である。（4-m^2=0の時）

まとめ

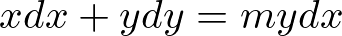
$\begin{align*} xdx+ydy&=mydx \end{align*}$

(mは任意の実数)

この微分方程式の一般解は、

4-m^2<0(m>2,m<-2）の時、(B-3)

4-m^2>0(-2<0>2）の時、（C-4)

4-m^2=0(m=±2)の時、（D-4）

である。

過去の記事

feynmandiagram.hatenablog.com

2019-03-06

ディラック方程式は負エネルギー解の問題を解決しない

物理学

クライン・ゴルドン方程式では、確率保存則の式が上手く作れないという問題と、負エネルギー解の問題がある。

以前の記事で書いたように、ディラックの方程式は、確率保存則の問題を解決する。

feynmandiagram.hatenablog.com

しかし、ディラックの方程式は負エネルギー解の問題を解決することが出来ない。

今回はそのことについて説明していきたいと思う。

ディラック方程式は負エネルギー解の問題を解決しない

ディラック方程式は負エネルギー解の問題を解決しない

数式群（A）

$\begin{align} &i \frac{\partial}{\partial t} \psi(x, t)=-i \bm{\alpha}\cdot \nabla \psi(x, t)+m \beta \psi(x, t)\\ &\psi(x)=w(p) e^{-i p x}\ \ \ (px\equiv Et-\bm{p}\cdot\bm{x})\\ &(E-\bm{\alpha}\cdot \bm{p}-m \beta) w(p)=0\\ &\omega(p)\neq0\to |E-\bm{\alpha}\cdot \bm{p}-m \beta|=\left| \begin{array}{cc}{E-m} & {-\bm{p}\cdot \bm{\sigma}} \\ {-\bm{p}\cdot \bm{\sigma}} & {E+m}\end{array}\right|=0\\ &p \equiv|\boldsymbol{p}|,\bm{p}=(0,0, p)\\ &\left| \begin{array}{cccc}{E-m} & {0} & {-p} & {0} \\ {0} & {E-m} & {0} & {p} \\ {-p} & {0} & {E+m} & {0} \\ {0} & {p} & {0} & {E+m}\end{array}\right|\nonumber\\ &=(E-m) \left| \begin{array}{ccc}{E-m} & {0} & {p} \\ {0} & {E+m} & {0} \\ {p} & {0} & {E+m}\end{array}\right|-p \left| \begin{array}{ccc}{0} & {-p} & {0} \\ {E-m} & {0} & {p} \\ {p} & {0} & {E+m}\end{array}\right|\nonumber\\ &=\left(E^{2}-p^{2}-m^{2}\right)^{2}\nonumber\\ &=\left(E^{2}-\bm{p}^{2}-m^{2}\right)^{2}=0\\ &E=\sqrt{\bm{p}^{2}+m^{2}}\ \ or\ \ E=-\sqrt{\bm{p}^{2}+m^{2}} \end{align}$

（１）はｎ＝２のディラック方程式。（スピン1/2のフェルミオンを記述する方程式）

（２）は確定した運動量に対する平面波（ω(p)はスピノル）

（２）を（１）に代入すると、（３）を得る。

（３）において、ω(p)≠０より、係数行列の行列式が０でなくてはならない（（４））

（５）では平面波の運動量ベクトルの向きにｚ軸をとり、ｐを新たに定義しなおした。（このｐは（２）で用いたｐとは異なる）。

（５）をもとに（４）を計算すると、（６）のようになる。

（６）より、（７）が導かれる。

（７）では、負エネルギー解が存在する。

この二つのエネルギーに対する解は独立であり、この二つの解の重ね合わせで一般解を表現することになるので、負エネルギー解は必要。

したがって、負エネルギー解の問題は解決されていない。

今回の記事はこれで終わりです。

過去の記事

feynmandiagram.hatenablog.com

物理人、世界を語る

ニュース、日々の出来事、物理学の解説、物理に関する紹介、考えたことについてつぶやきます。

大学物理の内容を整理する

力学

電磁気学

熱力学

振動と波動

物理数学

解析力学

統計力学

相対性理論

量子力学

Windowsの機能、使いこなせてますか？

Snipping tool

ペイント３D

検索流入の割合が３０%を超えました！【ブログ歴約３か月】

スピノルの慣性系同士の変換

スピノルの変換が満たす条件を求める

Sが満たすべき条件から、Sを求める

ディラック方程式を共変形式っぽい形に直す

ディラック方程式を共変形式っぽい形に直す

同次形の微分方程式の例題（xdx+ydy=mydx)

今回解く同次形の微分方程式

微分方程式を変数分離して解く

まとめ

ディラック方程式は負エネルギー解の問題を解決しない

ディラック方程式は負エネルギー解の問題を解決しない