同次形の微分方程式の例題(xdx+ydy=mydx)
前回、こちらの記事で、同次形の微分方程式ならば変数分離することが出来て積分計算により微分方程式の解を求めることが出来るということについて触れました。
今回は同次形の微分方程式の例題について解いていきたいと思います。
今回解く同次形の微分方程式
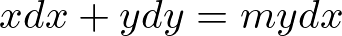
mは任意の実数です。
微分方程式を変数分離して解く
数式群(A)
%26%3Dmuxdx%5C%5C%0Ax(1%2Bu%5E2-mu)dx%26%3D-ux%5E2du%5C%5C%0A%5Cfrac%7Bd%20x%7D%7Bx%7D%26%3D%5Cfrac%7Bu%20d%20u%7D%7Bm%20u-1-u%5E%7B2%7D%7D%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B-u%20d%20u%7D%7B1-m%20u%2Bu%5E%7B2%7D%7D%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B%5Cleft(-u%2B%5Cfrac%7B1%7D%7B2%7D%20m%5Cright)%20d%20u%7D%7B1-m%20u%2Bu%5E%7B2%7D%7D-%5Cfrac%7B%5Cfrac%7B1%7D%7B2%7D%20m%20d%20u%7D%7B1-m%20u%2Bu%5E%7B2%7D%7D%5C%5C%0A%5Cint%20%5Cfrac%7Bd%20x%7D%7Bx%7D%26%3D%5Cint%20%5Cfrac%7B-u%2B%5Cfrac%7B1%7D%7B2%7D%20m%7D%7B1-m%20u%2Bu%5E%7B2%7D%7D%20d%20u-%5Cint%20%5Cfrac%7B%5Cfrac%7B1%7D%7B2%7D%20m%7D%7B%5Cleft(u-%5Cfrac%7Bm%7D%7B2%7D%5Cright)%5E%7B2%7D%2B%5Cfrac%7B4-m%5E%7B2%7D%7D%7B4%7D%7D%20d%20u%5C%5C%0A%5Cln%20x%26%3D-%5Cfrac%7B1%7D%7B2%7D%20%5Cln%20%5Cleft(u%5E%7B2%7D-m%20u%2B1%5Cright)-%5Cfrac%7Bm%7D%7B2%7D%20%5Cint%20%5Cfrac%7B1%7D%7B%5Cleft(u-%5Cfrac%7Bm%7D%7B2%7D%5Cright)%5E%7B2%7D%2B%5Cfrac%7B4-m%5E%7B2%7D%7D%7B4%7D%7D%20d%20u%5C%5C%0AA%20%26%5Cequiv%20%5Cint%20%5Cfrac%7B1%7D%7B%5Cleft(u-%5Cfrac%7Bm%7D%7B2%7D%5Cright)%5E%7B2%7D%2B%5Cfrac%7B4-m%5E%7B2%7D%7D%7B4%7D%7D%20d%20u%0A%5Cend%7Balign%7D&f=c&r=300&m=p&b=f&k=f)
(1)は今回解く微分方程式。
(2)は変数分離するためのuの導入。(前の記事で説明した)
(3)は(2)より導かれる関係式。
(4)は(2)、(3)を(1)に代入したもの。
(5)は(4)を整理したもの。
(6)は(4)を変数分離したもの。
(7)は(6)の両辺を積分したもの。
(8)は(7)の両辺を計算したもの。
(9)は(8)の右辺2項目に出てくる積分をAと定義した。
(9)のAさえ求まれば微分方程式の解が求まるのだが、
(9)のAは、4-m^2の符号によって、計算方法が変わってくる。
Aを4-m^2の符号によって場合分けしながら、計算していこう。
(i)4-m^2<0の時
数式群(B)
%5E%7B2%7D%2B%5Cfrac%7B4-m%5E%7B2%7D%7D%7B4%7D%7D%20d%20u%5Cnonumber%5C%5C%0A%26%3D%5Cint%20%5Cfrac%7B1%7D%7B%5Cleft(u-%5Cfrac%7Bm%7D%7B2%7D%2B%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%5Cright)%5Cleft(u-%5Cfrac%7Bm%7D%7B2%7D-%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%5Cright)%7D%20d%20u%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%20%5Cint%5Cleft(%5Cfrac%7B1%7D%7Bu-%5Cfrac%7Bm%7D%7B2%7D-%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%7D-%5Cfrac%7B1%7D%7Bu-%5Cfrac%7Bm%7D%7B2%7D%2B%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%7D%5Cright)%20d%20u%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%20%5Cln%20%5Cfrac%7Bu-%5Cfrac%7Bm%7D%7B2%7D-%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%7D%7Bu-%5Cfrac%7Bm%7D%7B2%7D%2B%5Cfrac%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7B2%7D%7D-%5Cfrac%7B2%7D%7Bm%7D%5Cln%20c%20%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B1%7D%7B%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%20%5Cln%20%5Cfrac%7B2%20y-%5Cleft(m%2B%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D%7B2%20y-%5Cleft(m-%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D-%5Cfrac%7B2%7D%7Bm%7D%5Cln%20c%5C%5C%0A%5Cln%20x%20%26%5Csqrt%7B1-m%20u%2Bu%5E%7B2%7D%7D%2B%5Cfrac%7Bm%7D%7B2%20%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%20%5Cln%20%5Cfrac%7B2%20y-%5Cleft(m%2B%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D%7B2%20y-%5Cleft(m-%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D%3D%5Cln%20c%5C%5C%0A%26%5Cleft(%5Cfrac%7B2%20y-%5Cleft(m%2B%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D%7B2%20y-%5Cleft(m-%5Csqrt%7Bm%5E%7B2%7D-4%7D%5Cright)%20x%7D%5Cright)%5E%7B%5Cfrac%7Bm%7D%7B2%5Csqrt%7Bm%5E%7B2%7D-4%7D%7D%7D%20%5Csqrt%7Bx%5E%7B2%7D-m%20x%20y%2By%5E%7B2%7D%7D%3Dc%0A%5Cend%7Balign%7D&f=c&r=300&m=p&b=f&k=f)
(1)は(A-9)のAの計算。(-(2/m)lnc は積分定数)
(1)を(A-8)に代入して整理すると、(2)の式になる。
(2)にu=y/xを代入して左辺と右辺のlnの中身を比較することで、(3)の式を得る。
(3)が微分方程式の一般解である。(4-m^2<0の時)
(ii)4-m^2>0の時
数式群(C)
%5E%7B2%7D%2B%5Cfrac%7B4-m%5E%7B2%7D%7D%7B4%7D%7D%20d%20u%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B2%7D%7B%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%20%5Carctan%20%5Cfrac%7B2%20u-m%7D%7B%5Csqrt%7B4-m%5E%7B2%7D%7D%7D-%5Cfrac%7B2%7D%7Bm%7D%20C%5Cnonumber%5C%5C%0A%26%3D%5Cfrac%7B2%7D%7B%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%20%5Carctan%20%5Cfrac%7B2%20y-m%20x%7D%7Bx%20%5Csqrt%7B4-m%5E%7B2%7D%7D%7D-%5Cfrac%7B2%7D%7Bm%7D%20C%5C%5C%0A%5Clog%20x%20%5Csqrt%7B1-m%20u%2Bu%5E%7B2%7D%7D%26%3DC-%5Cfrac%7Bm%7D%7B%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%20%5Carctan%20%5Cfrac%7B2%20y-m%20x%7D%7Bx%20%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%5C%5C%0A%5Clog%20%5Csqrt%7Bx%5E%7B2%7D-m%20x%20y%2By%5E%7B2%7D%7D%26%3DC-%5Cfrac%7Bm%7D%7B%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%20%5Carctan%20%5Cfrac%7B2%20y-m%20x%7D%7Bx%20%5Csqrt%7B4-m%5E%7B2%7D%7D%7D%0A%5Cend%7Balign%7D&f=c&r=300&m=p&b=f&k=f)
(1)は公式。
(2)は、(1)の公式をもとに、(A-9)のAを計算したもの。(最後の式でu=y/xを代入している)(-(2/m)Cは積分定数)
(3)は(2)を(A-8)に代入して整理したもの。
(4)は(3)においてu=y/xを代入したもの。
(4)が微分方程式の一般解である。(4-m^2>0の時)
(iii)4-m^2=0の時
数式群(D)
%5E%7B2%7D%7D%5C%20%5C%20(m%3D%5Cpm2)%5C%5C%0A%5Clog%20x%26%3DC-%5Clog%20(1%5Cmp%20u)-%5Cfrac%7B1%7D%7B1%5Cmp%20u%7D%5C%5C%0A%5Clog%20x(1%5Cmp%20u)%26%3DC-%5Cfrac%7B1%7D%7B1%5Cmp%20u%7D%5C%5C%0A%5Clog%20(x%5Cmp%20y)%26%3DC-%5Cfrac%7Bx%7D%7Bx%5Cmp%20y%7D%0A%5Cend%7Balign%7D&f=c&r=300&m=p&b=f&k=f)
(1)は(A-6)をm=±2の場合に計算したもの。
(2)は(1)の両辺を積分したもの。
(3)は(2)を整理したもの。
(4)は(3)にu=y/xを代入したもの。
(4)が微分方程式の一般解である。(4-m^2=0の時)
まとめ
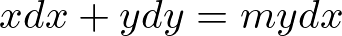
(mは任意の実数)
この微分方程式の一般解は、
4-m^2<0(m>2,m<-2)の時、(B-3)
4-m^2>0(-2<0>2)の時、(C-4)
4-m^2=0(m=±2)の時、(D-4)
である。
過去の記事