2019-03-04

久々に料理作りました。

日常

久しぶりに料理を作りました。

外食に比べて安くつくのでいいですね。

野菜炒めとトマトとご飯を食べました。

f:id:feynmandiagram:20190304112316j:plain

まあまあ旨し！

2019-03-04

リッカチの微分方程式の特殊な場合の解法

物理学

今回は、リッカチの微分方程式の特殊な場合の解法について説明したいと思います。

リッカチの微分方程式とは

数式群（A）

ｍ、aは定数。

（１）は（２）においてｍ＝－２としたときの式。

$\begin{align} d z+z^{2} d x=\frac{a d x}{x^{2}}\ \ (a \neq 0)\\ d z+z^{2} d x=a x^{m} d x \end{align}$

リッカチの微分方程式とは、（２）の式のことを言う。

リッカチの微分方程式が解けるのは、ｍが特定の形の値の場合に限られる。

今回は、その中でも、ｍ＝－２としたときの微分方程式（１）について解く。

同次形の微分方程式は変数分離形にできる

数式群（B）

$\begin{align} \frac{d y}{d x}&=f\left(\frac{y}{x}\right)\\ \frac{y}{x}&=u\\ \frac{d y}{d x}&=\frac{d x}{d x} u+x \frac{d u}{d x}=u+x \frac{d u}{d x}\\ x \frac{d u}{d x}&=f(u)-u\\ \frac{d u}{f(u)-u}&=\frac{d x}{x} \end{align}$

（１）の形の微分方程式は同次形とよばれる。

（２）のように変数uを導入する。

（３）は（１）の左辺を（２）より計算したもの。

（４）は（１）に（３）を代入したもの。

（５）は（４）を変形したもの。（変数分離形になっている）

（１）は変数uを用いて（５）のように変数分離形にすることができることが分かった。

変数分離形にすることが出来れば、両辺を積分するだけで微分方程式を解くことが出来る。

つまり、微分方程式を解くことができるかどうかという問題が、積分計算をすることができるかという問題に置き換わる。

(A-1)は同次形に変形できる

数式群（C）

$\begin{align} z&=\frac{1}{y}\\ d z&=-\frac{d y}{y^{2}}\\ -\frac{d y}{y^{2}}+\frac{d x}{y^{2}}&=\frac{a d x}{x^{2}}\\ x^{2} d y&=\left(x^{2}-a y^{2}\right) d x\\ \frac{d y}{d x}&=1-a \left(\frac{x}{y}\right)^{2} \end{align}$

（A-1）は同次形の形をしていない。

適当な変数変換により、（A-1）は同次形にすることが出来ることを示す。

（１）ように変数変換を行うと、（２）のような関係が分かる。

（２）を（A-1）に代入すると、（３）を得る。

（４）は（３）を変形したもの。

（５）は（４）を変形したもの。

従って、z=1/yとおくことで、(A-1)を（５）のように同次形にすることが出来た。

変数分離形にして解く

(A-1)を同次形にすることが出来たので、数式群（B)の議論から、（A-1)を変数分離形にして解くことが出来るという事が分かる。

数式群（D）

$\begin{align} \frac{d y}{d x}&=1-a\left(\frac{y}{x}\right)^2\\ y&=u x\\ d y&=u d x+x d u\\ u d x+x d u&=\left(1-a u^{2}\right) d x\\ xdu&=\left(1-au^2-u\right)dx\\ 1-au^2-u&=0\\ z&=\frac{1}{ux} \end{align}$

(1)は（C-5）の式。（（A-1)を変形したもの）

（２）は（B-2)。

（３）は（２）より導かれる関係式。

（４）は（３）を（１）に代入したもの。

（５）は（４）を変形したもの。

ここで、uを（６）を満たす定数とすると、（５）は満たされる。

すなわち、（１）の微分方程式は（７）の解を持つ。

uが(D-6)を満たす定数ではないときを考える。

このとき、（C-5)は（１）のように変形される。

数式群（E）

$\begin{align} \frac{d x}{x}&=\frac{d u}{1-a u^{2}-u}\\ \log x&=-\int \frac{d u}{a u^{2}+u-1}\nonumber\\ &=-\frac{1}{a} \int \frac{d u}{u^{2}+\frac{1}{a} u-\frac{1}{a}}\nonumber\\ &=-\frac{1}{a} \int \frac{d u}{\left(u+\frac{1}{2 a}\right)^{2}-\frac{1+4 a}{4 a^{2}}} \end{align}$

また、（１）の両辺を積分すると、（２）の式になる。

したがって、（２）の積分を計算すれば、uが（C-6)を満たす定数ではないときの（A-1)の微分方程式の解を求めることが出来る。

ここで、（２）の右辺の積分では、１＋４aの符号に応じて計算の仕方が変わる。

(i)4a+1=0の場合

数式群（F） $\begin{align} \log x&=-\frac{1}{a} \int \frac{d u}{\left(u+\frac{1}{2 a}\right)^{2}-\frac{1+4 a}{4 a^{2}}}\\ \log x&=4 \int \frac{d u}{(u-2)^{2}}\nonumber\\ &=-\frac{4}{u-2}+C\\ u&=\frac{y}{x}\\ \log x&=\frac{4 x}{2 x-y}+C\\ y&=\frac{1}{z}\\ \log x&=\frac{4 x z}{2 x z-1}+C \end{align}$

（１）は（D-2）。

4a+1=0ならば、（１）の右辺は（２）のように計算される。

（３）は（D-2)。

（３）を（２）に代入すると、（４）になる。

（５）は(C-1)。

（５）を（４）に代入すると、（６）の式を得る。

（６）が（A-1)の微分方程式の解である。

(ii)4a+1>0の場合

数式群（G）

$\begin{align} \log x&=-\frac{1}{a} \int \frac{d u}{\left(u+\frac{1}{2 a}\right)^{2}-\frac{1+4 a}{4 a^{2}}}\\ \log x&=-\frac{1}{a} \cdot \frac{a}{\sqrt{1+4 a}} \int\left\{\frac{1}{u+\frac{1}{2 a}-\frac{\sqrt{1+4 a}}{2 a}}-\frac{1}{u+\frac{1}{2 a}+\frac{\sqrt{1+4 a}}{2 a}}\right\}\nonumber\\ &=-\frac{1}{\sqrt{1+4 a}}\left\{\log \left(u+\frac{1}{2 a}-\frac{\sqrt{1+4 a}}{2 a}\right)-\log \left(u+\frac{1}{2 a}+\frac{\sqrt{1+4 a}}{2 a}\right)\right\}+C\nonumber\\ &=-\frac{1}{\sqrt{1+4 a}} \log \frac{u+\frac{1-\sqrt{1+4 a}}{2 a}}{u+\frac{1+\sqrt{1+4 a}}{2 a}}+C\nonumber\\ &=-\frac{1}{\sqrt{1+4 a}} \log \frac{2 a u+1-\sqrt{1+4 a}}{2 a u+1+\sqrt{1+4 a}}+C\\ u&=\frac{y}{x}\\ e^{C} &\rightarrow C \end{align}$

$\setcounter{equation}{4} \begin{align} x\left(\frac{2 a y+(1-\sqrt{1+4 a}) x}{2 a y+(1+\sqrt{1+4 a}) x}\right)^{\frac{1}{\sqrt{1+4 a}}}&=C\\ y&=\frac{1}{z}\\ x\left(\frac{2 a+(1-\sqrt{1+4 a}) x z}{2 a+(1+\sqrt{1+4 a}) x z}\right)^{\frac{1}{\sqrt{1+4 a}}}&=C \end{align}$

（１）は（D-2）。

（２）は（１）の右辺の積分計算

（３）は（D-2)。

（４）は定数e^CをあらためてCと表記することを示す。

（３）、（４）を（２）に代入すると、（５）を得る。

（６）は(C-1)。

（５）に（６）を代入すると、（７）を得る。

（７）が（A-1)の微分方程式の解である。

(iii)4a+1<0の場合

数式群（H）

$\begin{align} \log x&=-\frac{1}{a} \int \frac{d u}{\left(u+\frac{1}{2 a}\right)^{2}-\frac{1+4 a}{4 a^{2}}}\\ \int \frac{d X}{X^{2}+A^{2}}&=\frac{1}{A} \arctan \frac{X}{A}\\ X&=u+\frac{1}{2 a}, \quad A=\frac{\sqrt{-1-4 a}}{2 a}\\ u&=\frac{y}{x}\\ \log x=&-\frac{1}{a} \cdot \frac{2 a}{\sqrt{-1-4 a}} \arctan \frac{2 a}{\sqrt{-1-4 a}}\left(\frac{2 a y+x}{2 a x}\right)+C\nonumber \\&=-\frac{2}{\sqrt{-1-4 a}} \arctan \frac{2 a y+x}{x \sqrt{-1-4 a}}+C\\ y&=\frac{1}{z}\\ \log x&=-\frac{2}{\sqrt{-1-4 a}} \arctan \frac{2 a+x z}{x z \sqrt{-1-4 a}}+C \end{align}$

（１）は（D-2）。

（２）は一般に成り立つ式。

（４）は（D-2）である。

（２）の公式で（３）のようにして（１）の右辺を計算し、（４）を代入すると、（５）のようになる。

（６）は(C-1)。

（６）を（５）に代入すると、（７）の式を得る。

（７）が（A-1)の微分方程式の解である。

まとめ

リッカチの微分方程式（A-2)において、ｍ＝－２としたときの微分方程式（A-1）の解を今回求めた。

その解は、（D-7）に加えて、

4a+1=0の場合は（F-6)、

4a+1>0の場合は（G-7)、

4a+1<0の場合は（H-7)

である。

今回の記事はこれで終わりです。

物理に関する過去記事。

feynmandiagram.hatenablog.com

2019-03-03

クライン・ゴルドン方程式の導出

物理学

今回は、クライン・ゴルドン方程式がどのように導かれるかということについて説明したいと思います。

クライン・ゴルドン方程式は、量子力学に特殊相対性理論の概念を混ぜたときに出てくる式です。

自然単位系を用います

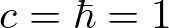
$\begin{align*} c=\hbar=1 \end{align*}$

以降の議論では、光速と、ディラック定数を１とする、自然単位系を用いています。

シュレディンガー方程式の復習

数式群（A）

$\begin{align} i \frac{\partial}{\partial t} \psi(x, t)&=H \psi(x, t) \quad(H=-\Delta /(2 m\rfloor)\\ E&=p^{2} /[2 m]\\ E \rightarrow i \partial / \partial t,& \quad p \rightarrow-i \nabla \end{align}$

（１）はシュレディンガー方程式。

（２）の式に、量子化の手続き（３）を施すことで、（１）の式を得ることが出来る。

シュレディンガー方程式の導出がヒントになる

シュレディンガー方程式の導出をヒントに、特殊相対性理論の要素をとりこんだ量子力学の式である、クライン・ゴルドン方程式を導くことを考えていこう。

クライン・ゴルドン方程式の導出

数式群（B）

$\begin{align} E&=\sqrt{p^{2}+m^{2}}\\ E^{2}&=p^{2}+m^{2}\\ \frac{\partial^{2}}{\partial t^{2}} \psi(x, t)&=\left(\Delta-m^{2}\right) \psi(x, t)\\ \square &\equiv \partial^{2} / \partial t^{2}-\Delta\\ \left(\square+m^{2}\right) \psi(\boldsymbol{x}, t)&=0 \end{align}$

（１）は相対論的力学におけるエネルギー。

（１）を量子化して方程式を立てたいところだが、ルートが入っているので、このままじゃ上手く式をたてることができない。

そこで、（２）のように、（１）の式を二乗してみる。

そうして、（A-3）の量子化の手続きを施し、（２）の式を量子化すると、（３）の式を得ることが出来る。

また、（４）のように、ダランベール演算子（四角の記号）とよばれるものを定義すると、（３）の式は、

（５）のようにあらわされる。

（５）（＝（３））が、クライン・ゴルドン方程式である。

今回の記事はこれで終わりです。

量子力学の過去記事。

feynmandiagram.hatenablog.com

2019-03-03

ふぃくしのん（ピアノYoutuber)さんの紹介

おすすめYoutuber紹介

移転しました。

こんにちは、マーキュリーです。

今回は私のおすすめピアノYoutuber、ふぃくしのんさんについて紹介していきたいと思います。

ふぃくしのんさんってどんな人？
ふぃくしのんさんのおすすめ動画
チャンネル登録者、再生回数など

ふぃくしのんさんってどんな人？

趣味でピアノを弾いておられる方。ピアニストじゃなく一般人の方です。

ふぃくしのんさんのおすすめ動画

www.youtube.com

チャンネル登録者、再生回数など

こちらのサイトに詳しく載っています。

ふぃくしのん / phyxinonの年収・収入は？再生回数・登録者数ランキングを予想！ | YouTuberリアル

私の調査では、２０１９年３月３日現在、

チャンネル登録者数：９８６０２人

再生回数：約１６００万回

動画数：１４２

です。

今回の記事はこれで終わりです。

他のピアノYoutuber紹介記事

feynmandiagram.hatenablog.com

2019-03-02

数式を簡単に書く方法（ブログ記事、パワーポイント発表などに使える）

理系のための記事

数式をウェブ上に書くには様々な方法があります。

私は、ときたま数式を使ったブログ記事を書きます。

私のブログでは、数式を画像化し、それをブログ記事に貼り付けることによって数式を書いています。

画像化するときは、「TeXclip」というアプリを用いています。（無料、インストールの必要なし）

feynmandiagram.hatenablog.com

TeXclipでは、LaTeXのコマンドを打ちこみ、画像変換のボタンをクリックするだけで、簡単に数式を画像化することが出来ます。

今回は、主に、LaTeXのコマンドをうちこむ簡単な方法についてお知らせしたしたいと思います。

つまり、私の記事のように、ブログ記事に数式を書きたければ、

１．今回お知らせした方法で数式コマンドをTeXclipの中に書く

２．TeXclipで画像変換のボタンをクリックすることで数式を画像に変換する。

３．画像化した数式をブログ記事に貼り付ける。

という事をしていただければいいです。

この一連の流れは、パワーポイントに画像化した数式を貼り付ける際など、様々な状況に使えるのではないかと思います。

また、LaTexのコマンドを簡単にうちこむ方法を知ることができれば、論文を書く際の数式をうちこむ手間も減るでしょう。

では説明していきます。

１．写真を撮る
２．Mathpixというツール（無料、インストールの必要あり）を用いて、手書きの数式をLaTeXコマンドに変換する
３．数式を画像化して、ブログに貼り付ける
まとめ

１．写真を撮る

f:id:feynmandiagram:20190302092048p:plain

まずは、ブログ記事やパワーポイントでの発表、LaTeXで書く論文に使いたい数式を、まとめてコピー用紙（紙なら何でもいいですがコピー用紙が紙の中で一番安い）に書きます。

２．Mathpixというツール（無料、インストールの必要あり）を用いて、手書きの数式をLaTeXコマンドに変換する

feynmandiagram.hatenablog.com

上の、以前の記事でも紹介しましたが、インターネットサイト上の数式や手書きの数式などを読み取って、LaTeXのコマンドに変換してくれる、Mathpixというツールがあります。

これをまずは

https://mathpix.com/

からインストールしましょう。

インストール中には英語で書かれた文章が多く出てきますが、直感に従ってインストールしていけば簡単にインストールできます。

インストールした後は、

変換したい数式が画面上にある状況で、

Ctrl+Alt+M

を押します。

そうすると、下の画像のように、画面が暗くなります。

f:id:feynmandiagram:20190302095558p:plain

また、クリックポインターが十字のポインターに代わります（上の画像上には写されていません）。

その十字ポインターを使って、下の画像のように、変換したい数式を囲みます。（同時に複数の数式を囲んで変換することは出来ません）

f:id:feynmandiagram:20190302095837p:plain

そうすると、自然に、次のような画面が出てきます。

f:id:feynmandiagram:20190302092749p:plain

少し違う部分は、次のように手直ししてあげましょう。（LaTeXのコマンドを知っている必要あり）

f:id:feynmandiagram:20190302092440p:plain

手直しができたら、

f:id:feynmandiagram:20190302100747p:plain

これの一番上のCopyのところをクリックして、コマンドをコピーします。

次に、数式を画像化する手順を話します。

３．数式を画像化して、ブログに貼り付ける

TeXclip（TeXclip）の画面に移動しましょう。

そこで、このように、数式を打ち込む形式（equationなのか、alignなのか、align*なのか、など）だけ指定してあげます。

f:id:feynmandiagram:20190302101828p:plain

ここで、先ほどMathjaxを使ってコピーしたLaTexのコマンドを、Ctrl+V（貼り付けコマンド）によって、次のように貼り付けた後、Generateボタンをクリックし、画像に変換します。その後、画像のところで右クリックをします。

f:id:feynmandiagram:20190302105952p:plain

そしたら、画像をコピーをクリックし、ブログ記事にCtrl+Vを使って貼り付けると、

f:id:feynmandiagram:20190302103141p:plain

こんな感じで画像化した数式を貼り付けることが出来ます。

一番最初に書いた手書きの数式を全部Mathjaxを使ってLaTeXのコマンドに変換し、TeXclipに貼り付けると、こんな感じになります。

f:id:feynmandiagram:20190302103932p:plain

しかし、Mathjaxをつかった、手書きの数式の画像の、LaTeXコマンドへの変換が上手くいっていないため、数式が上手く表示されていませんね。

コマンドの間違いを、こんな感じに、TeXclip上で手直ししてあげましょう。最初の説明ではMathjaxの画面で手直しを行いましたが、Mathjaxでは表示できる数式の種類に限界があります。例えば太字などは表示できません。そのため、TeXclipに数式コマンドをコピペしてから、TeXclip上で手直しを行ったほうが手直しがしやすいです。

f:id:feynmandiagram:20190302104820p:plain

そして出来た画像をコピペしてあげれば、

$\begin{align*} g_{\mu \nu}=g^{\mu \nu}=\left( \begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {-1} & {0} & {0} \\ {0} & {0} & {-1} & {0} \\ {0} & {0} & {0} & {-1}\end{array}\right)\\ \frac{\partial}{\partial t} \rho(\bm{x}, t)+\operatorname{div} j(\bm{x}, t)=0\\ i \frac{d}{\partial t}\psi(\bm{x}_, t)=H \psi(\bm{x}, t)\\ \mathcal{L}=-\frac{1}{4}\left(F_{\mu \nu}^{\alpha}\right)^{2}+\frac{1}{2}\left(D_{\mu} \phi\right)^{2}-V(\phi) \end{align*}$

こんな感じで数式を表示することが出来ます。

さらに、数式番号をつけて数式を表示すれば、こんな感じの、小さなサイズになります。

$\begin{align} g_{\mu \nu}=g^{\mu \nu}=\left( \begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {-1} & {0} & {0} \\ {0} & {0} & {-1} & {0} \\ {0} & {0} & {0} & {-1}\end{array}\right)\\ \frac{\partial}{\partial t} \rho(\bm{x}, t)+\operatorname{div} j(\bm{x}, t)=0\\ i \frac{d}{\partial t}\psi(\bm{x}_, t)=H \psi(\bm{x}, t)\\ \mathcal{L}=-\frac{1}{4}\left(F_{\mu \nu}^{\alpha}\right)^{2}+\frac{1}{2}\left(D_{\mu} \phi\right)^{2}-V(\phi) \end{align}$